ゲーム AI の難易度とは?

「ゲーム AI の進化と歴史」で紹介したとおり、ゲーム AI は AI 研究の進展にともなって進化しています。ゲームは、AI 研究にとって最も重要な検証プラットフォームとされており、難易度や複雑さの度合いが異なる、様々なジャンルのゲームが AI でプレイできるようになっています。

現在、AI は、ポーカーやブリッジ、麻雀など、これまでに対戦してきた将棋類 (バックギャモン、チェッカー、チェス、囲碁など) よりも、さらに難易度の高いゲームにおいてチャレンジしています。なぜこのようなゲームは難易度が高いのか、異なるジャンルのゲームの複雑さと難易度をどう測るのかを解説します。

ゲームの複雑さ≠ゲームの難易度

まず最初に、ゲームの「複雑さ」と「難易度」は、等しくないという点に留意ください。ゲームの難易度は、ゲーム自体の複雑さ以外に、戦略など数多くの要素に関係しています。つまり、数学的に複雑なゲームが、必ずしも難しいとは限らないのです。一般的に、把握できる情報の量によって、ゲームは、「完全情報ゲーム (Perfect-Information Games)」と「不完全情報ゲーム (Imperfect-Information Games)」の 2 種類に分類されます。すべてのゲームプレイヤーが、ゲームのあらゆる段階において (相手も含めて) ゲームに関する状態、およびこれから継続していく情報を把握できる場合、このゲームを「完全情報ゲーム」と呼び、そうではないものを、「不完全情報ゲーム」と呼びます。たとえば、囲碁やチェスなど将棋類ゲームは、対局者は碁盤にあるすべての情報が見えるため、「完全情報ゲーム」に属します。一方、ポーカーやブリッジ、麻雀などは、ゲーム参加者はお互いが出した手札は見えますが、相手の手札や伏せたままの残り札は見えません。参加者それぞれが把握している情報に格差があるため、「不完全情報ゲーム」に属しています。

「完全情報ゲーム」と「不完全情報ゲーム」の難易度は、異なる尺度を用いて測るのが一般的です。「完全情報ゲーム」では、ゲームの複雑さによってその難易度が決まることが多いため、状態空間複雑性 (State-Space Complexity) とゲーム木複雑性 (Game-Tree Complexity) で難易度を測ることができます。「不完全情報ゲーム」の場合、隠されている情報によってゲームの難易度が大きく影響されてしまうため、情報集合 (Information Set) の数とその平均的な大きさで測っています。

完全情報ゲーム: 状態空間複雑性とゲーム木複雑性

状態空間複雑性 (State-Space Complexity)

ゲームの状態空間複雑性 (SSC) とは、ゲームの初期局面から到達できるルール適合のすべての局面数を示しています。たとえば、将棋類ゲームでは駒を 1 つ移動させ、もしくは駒を 1 つ取るたびに、新しい盤面ができます。そういったすべての盤面状態はゲームの状態空間になります。通常、ゲームの状態空間の大きさを精確に計算するのは難しく、概略を見積もることしかできません。最も使われる見積もり方法として、ルール不適合やゲームに出てくるはずのない局面も含めて状態空間の上界 (Upper Bound) を計算する方法があります。たとえば、囲碁の局面数上界の見積もりをする時は、盤面がすべて白石の場合とすべて黒石の場合といった極端な情況も含めて考えます。

実際、三目並べ (〇 × ゲーム) のような簡単なゲームでも、状態空間が大きくなります。三目並べの碁盤には 9 (3 x 3) の格子があり、各格子には X、O、空白という 3 つの状態があります。そのため、局面数は 3 の 9 乗である、19863 となります。もちろん、これは状態空間の上界なので、ルール不適合の状態も多く含まれています。このように、三目並べの状態空間複雑性は約 10⁴ (19863 ≈ 10⁴) であることがわかります。この計算方法をより大きな碁盤とより複雑な棋類ゲームへ展開してみましょう。たとえば、囲碁の場合、碁盤には 361 (19×19) の格子があり、各格子には白石か黒石を入れるか、空白の状態とします。前述の方法で計算すると囲碁の状態空間複雑性は約 10¹⁷² (3³⁶¹ ≈ 10¹⁷²) であることがわかります。表 1 に、よくある完全情報ゲームに属する将棋類ゲームの状態空間複雑性を示します。

ゲーム木複雑性 (Game-Tree Complexity)

ゲーム木複雑性 (GTC) はゲームのすべての到達経路の数を表しています。同じ状態の盤面に到達してもゲームの経路は必ず同じだと限らないため、ゲーム木複雑性は状態空間複雑性より遥かに高くなっています。たとえば、図 1 のように、三目並べの盤面に X が2つ、O が 1 つあるとします。この盤面に至るには、2 つの経路があります。最初の X の入れる場所によって経路が決まります。

状態空間と似たように、ゲーム木複雑性を精確に計算するのも難しくなっています。よく使われている方法として、その合理的な下界「GTC ≥ b^p 」の見積もりをしています。計算式の「b」は、ターンごとの合理移動可能の数を表し、「p」はゲームの平均的な長さを表しています。そこから、合理移動可能な数の多いゲームのほうが複雑だとわかります。また、ゲームの平均的な長さも、ゲーム木複雑性を影響する重要な要素となっています。

経験上、三目並べ、チェス、囲碁のターンごとの合理移動可能数はそれぞれ 4、35、250 で、ゲームの平均的な長さはそれぞれ 9、80、150 です。前述の計算式で計算すると、三目並べ、チェス、囲碁のゲーム木複雑性はそれぞれ 10⁵ (4⁹ ≈ 10⁵)、10¹²³ (35⁸⁰ ≈ 10¹²³)、10³⁶⁰ (250¹⁵⁰ ≈ 10³⁶⁰)であることもわかります。それ以外の完全情報ゲームに属する将棋類ゲームのゲーム木複雑性も表 1 に示します。

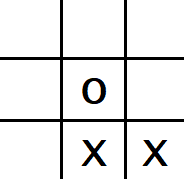
図 1: 三目並べ (〇 × ゲーム) — 図 1: 三目並べ(〇 × ゲーム)

ゲーム	状態空間複雑性	ゲーム木複雑性
三目並べ	10⁴	10⁵
チェッカー	10²¹	10³¹
チェス	10⁴⁶	10¹²³
中国象棋	10⁴⁸	10¹⁵⁰
五目並べ	10¹⁰⁵	10⁷⁰
囲碁	10¹⁷²	10³⁶⁰

表 1: 完全情報ゲームの状態空間複雑性とゲーム木複雑性

従来の「完全情報ゲーム」の中では、囲碁は、状態空間複雑性もゲーム木複雑性もほかのゲームより、はるかに高いことがわかります。2017 年、AlphaZero が MCTS と深層強化学習を利用して囲碁を含めた複数の完全情報ゲームを解いたことをきっかけに、学術研究では「不完全情報ゲーム」と「リアルタイムストラテジーゲーム」などがより注目されるようになっています。

不完全情報ゲーム: 情報集合数と平均的な大きさ

「不完全情報ゲーム」の場合も、「完全情報ゲーム」と同様にその状態空間複雑性とゲーム木複雑性を計算することができますが、情報が不完全で非対称的なため（たとえば、ポーカーと麻雀では相手の手札と伏せたままの残り札は把握できません）、参加者はゲームの実際の状態を分別することができません。たとえば、ポーカーでは自分が K を 2 枚持っていて、相手の手元にもいろいろな状態に対応するための手札を持っていますが、足元の具体的な状態は自分の中でもはっきりと分別することができません。そういった分別できないゲームの状態の集合を情報集合といいます。

「不完全情報ゲーム」での合理的なゲーム戦略は、ゲームの状態ではなく、情報集合に基づいて考えるべきであることは、極めて明らかです。なぜなら、観測できる情報からだけでは区別できないような状態の違いを考えても意味がないからです。これと同様に、不完全情報ゲームの難易度を測る時も、状態空間の大きさではなく、情報集合の数を尺度にすべきです。情報集合の数は通常、状態空間の数より少なく、特に完全情報ゲームの場合は、すべての情報を把握できるため、情報集合ごとにゲームの状態が 1 つしかありません。つまり、「完全情報ゲーム」の情報集合数は状態空間数と同じなのです。

情報集合の数以外に、情報集合の平均的な大きさという、もう一つ重要な尺度があります。これは、情報集合の中で区別できないゲームの状態の平均数のことです。1 対 1 のテキサスホールデム (ポーカー) を例として、もし自分の手札が AA で、相手の手札が AK もしくは AQ の場合、情報が不完全なため、実際 AK か AQ かが分別できません。その場合、AK と AQ の 2 つの状態を 1 つの情報集合に入れます。2 人テキサスホールデムの情報集合数は最大1326 (52 枚の札から 2 枚を出して: C₅₂²）で、約 10³。ここでおわかりかもしれませんが、情報集合数は不完全情報ゲームのありうるすべての戦略決定ノードの数を表しており、情報集合の平均的な大きさはゲームの各局面の裏に隠されている情報の数を表しています。明らかに、情報集合の平均的な大きさが大きいほど、未知で把握しきれない情報が多くなり、戦略決定が難しくなっています。実際、探索アルゴリズムを使えるかどうかは、情報集合の大きさと直接に関わっています。相手の隠されている状態が非常に多い場合、伝統的な探索アルゴリズムは基本的に使うことができません。そのため、情報集合の平均的な大きさもゲームの難易度を測る尺度として活用できます。

ゲーム	情報集合数	情報集合の平均的な大きさ
1 対 1 テキサスホールデム (制限付き)	10¹⁴	10³
1 対 1 テキサスホールデム (無制限)	10¹⁶²	10³
ブリッジ	10⁶⁷	10¹⁵
麻雀	10¹²¹	10⁴⁸

表 2 不完全情報ゲームの情報集合数と情報集合の平均的な大きさ

1 対 1 無制限テキサスホールデムは、情報集合数は多いのですが、未知の札は 2 枚しかないため、隠されている情報が少なく、情報集合の平均的な大きさが小さくなっています。ブリッジと麻雀の場合、各プレイヤーの手元に未知の手札が最大 13 枚あるため、テキサスホールデムより隠されている情報が遥かに多くなります。表 2 ではテキサスホールデム、ブリッジ、麻雀の情報集合数と情報集合の平均的な大きさを整理しています。

情報集合数と情報集合の平均的な大きさを尺度として、囲碁のような「完全情報ゲーム」を表 2 の「不完全情報ゲーム」と比べてみると、非常に面白い結果が出てきます。図 2 で示したように、囲碁とテキサスホールデムの情報集合の平均的な大きさはブリッジと麻雀より遥かに小さくなっています。AI が囲碁とテキサスホールデムのゲームに成功したのは、探索アルゴリズムの役割が大きいのです。それは、探索によってコンピューターの計算力を最大限に発揮できるからです。しかし、情報集合の平均的な大きさが大きくなると、環境の不確定性も上がってしまうため、伝統的な探索アルゴリズムはブリッジと麻雀に通用できなくなります。

これまで、ゲーム AI は、大部分の「完全情報ゲーム（チェスと囲碁など）」と、情報集合の平均的な大きさが小さい「不完全情報ゲーム (1 対 1 テキサスホールデムとマルチテキサスホールデム)」において、比較的理想的な形で勝利することができます。しかし、ブリッジと麻雀のような隠されている情報が多い「不完全情報ゲーム」については、新しい方法を見出さなければ、勝利することができません。AI アルゴリズムの研究者の探索はこれからも続いていくことでしょう。

図 2: 囲碁、テキサスホールデム、ブリッジ、麻雀の情報集合数と情報集合の平均的な大きさの比較

参考文献

[1] L.V. Allis, Searching for solutions in games and artificial intelligence, Ph.D. Thesis, University of Limburg, Maastricht, 1994.
[2] van den Herik, H., Uiterwijk, J. W. & van Rijswijck, J. Games solved: now and in the future. Artif. Intell. 134, 277–311 (2002).
[3] Game Complexity I: State-Space & Game-Tree Complexities
https://www.pipmodern.com/feed/state-space-game-tree-complexity
[4] Game Complexity III: Artificial Intelligence
https://www.pipmodern.com/feed/complexity-artificial-intelligence
[5] M. Johanson, Measuring the size of large no-limit poker games, Technical Report TR13-01, Department of Computing Science, University of Alberta (2013).
[6] Wiki: Game complexity https://en.wikipedia.org/wiki/Game_complexity

—

本ページのすべての内容は、作成日時点でのものであり、予告なく変更される場合があります。正式な社内承認や各社との契約締結が必要な場合は、それまでは確定されるものではありません。また、様々な事由・背景により、一部または全部が変更、キャンセル、実現困難となる場合があります。予めご了承下さい。